: Расширить свои знания в области доказательства неравенств. Познакомиться с неравенством Коши. Научиться применять изученные методы к доказательству неравенств.

Скачать:

Предварительный просмотр:

Государственное бюджетное общеобразовательное учреждение

средняя общеобразовательная школа №655

Приморского района Санкт-Петербурга

«Доказательство неравенств. Неравенство Коши»

2014г.

Ли Нина Юрьевна

8в класс

Аннотация…………………………………………………………………………………….3

Введение …………………………………………………………………………………….. 4

Историческая справка………………………………………………………………………..4

Неравенство Коши……………………………………………………………………………5

Доказательство неравенств…………………………………………………………………..7

Выводы исследования………………………………………………………………………..10

Список литературы……………………………………………………………………………11

Ли Нина

г. Санкт-Петербург, ГБОУ СОШ №655, 8 класс

«Доказательство неравенств. Неравенство Коши».

руководитель: Мороз Юлия Владимировна, учитель математики

Цель научной работы: Расширить свои знания в области доказательства неравенств. Познакомиться с неравенством Коши. Научиться применять изученные методы к доказательству неравенств.

ВВЕДЕНИЕ

«…основные результаты математики чаще выражаются не равенствами, а неравенствами».

Э. Беккенбах

Решением неравенств мы занимаемся на протяжении всего школьного курса. Неравенства можно решать графическим и аналитическим способом. Чтобы решить любое неравенство существует определенный алгоритм действий, поэтому данная задача является, скорее механическим действием, который не требует творческого подхода.

Напротив, доказательство неравенств требует неформального, вариативного подхода. Поэтому доказательство неравенств является наиболее интересным.

Однако, в школьном курсе математики доказательству неравенств уделяется очень мало внимания. Доказательство неравенств сводится к одному приему- оценке разности частей неравенства. Между тем, на математических олимпиадах часто встречаются задачи на доказательство неравенств с применением других способов и приемов (использование опорных неравенств, метод оценивания). На олимпиадах для школьников по математике также часто предлагаются неравенства, доказательство которых лучше выявляет способности и возможности учащихся, степень их интеллектуального развития. Кроме того, многие задачи повышенной сложности (из различных разделов математики) эффективно решаются с помощью неравенств.

Актуальность темы «Доказательство неравенств» бесспорна, так как неравенства играют фундаментальную роль в большинстве разделов современной математики, без них не может обойтись ни физика, ни астрономия, ни химия. Теория вероятности, математическая статистика, финансовая математика, экономика – все эти взаимосвязанные и обобщающие друг друга науки и в формулировках основных своих законов, и в методах их получения, и в приложениях, постоянно используют неравенства.

Доказательства неравенств помогают развить навык осмысления и применения приемов доказательства неравенств; умение применять их при выполнении различных задач; умение анализировать, обобщать и делать выводы; логически излагать мысли; творчески относится к делу.

Целью данной работа является расширение знаний в области методов и приемов доказательства неравенств.

Для достижения данной цели исследования мы поставили перед собой задачи:

• сбор информации из различных источников о приемах и методах доказательства неравенств;
• познакомится с неравенством Коши;
• Научится применять опорные неравенства к доказательству более сложных неравенств.

ИСТОРИЧЕСКАЯ СПРАВКА

Понятия «больше» и «меньше» наряду с понятием «равенство» возникли в связи со счетом предметов и необходимостью сравнивать различные величины. Понятиями неравенства пользовались еще древние греки. Архимед (III в. до н. э.), занимаясь вычислением длины окружности, установил, что «периметр всякого круга равен утроенному диаметру с избытком, который меньше седьмой части диаметра, но больше десяти семьдесят первых». Иначе говоря, Архимед указал границы числа π.

В 1557 г., когда Роберт Рекорд впервые ввел знак равенства, он мотивировал свое нововведение следующем образом: никакие два предмета не могут быть между собой более равными, чем два параллельных отрезка. Исходя из знака равенства Рекорда, другой английский ученый Гарриот ввел употребляемые и поныне знаки неравенства, обосновывая нововведение следующим образом: если две величины не равны, то отрезки, фигурирующие в знаке равенства, уже не параллельны, а пересекаются. Пересечение может иметь место справа (>) или слева (

Несмотря на то что знаки неравенства были предложены через 74 года после предложенного Рекордом знака равенства, они вошли в употребление намного раньше последнего. Одна из причин этого явления коренится в том, что типографии применяли в то время для знаков неравенства уже имевшуюся у них латинскую букву V, тогда как наборного знака равенства (=) у них не было, а изготовлять его тогда - было нелегко.

Знаки ≤ и ≥ ввел французский математик П. Буге.

НЕРАВЕНСТВО КОШИ

Применяемые для доказательства неравенств идеи почти столь же разнообразны, как и сами неравенства. В конкретных ситуациях общие методы часто приводят к некрасивым решениям. Но неочевидное комбинирование нескольких «базовых» неравенств удается лишь немногим. И, кроме того, ничто не мешает нам в каждом конкретном случае поискать более удобное, лучшее решение, нежели полученное общим методом. По этой причине доказательства неравенств нередко относят к области искусства. И как во всяком искусстве здесь есть свои технические приемы, набор которых весьма широк и овладеть всеми очень сложно.

Одним из таких «базовых» неравенств является неравенство Коши, указывающее на соотношение двух средних величин – среднего арифметического и среднего геометрического. Среднее арифметическое изучается в школьном курсе пятого класса и выглядит таким образом Среднее геометрическое впервые появляется в курсе геометрии восьмого класса - . В прямоугольном треугольнике таким свойством обладают три отрезка: два катета и перпендикуляр, опущенный из вершины прямого угла на гипотенузу.

Между этими двумя этими величинами существует удивительное соотношение, которое исследовали ученые. О. Коши, французский математик, пришел к выводу о том, что среднее арифметическое n неотрицательных чисел всегда не меньше среднего геометрического этих чисел.

Наряду с неравенством Коши полезно знать следствия из него:

Равенство достигается при a = b.

Неравенства верны, если выполняются условия a > 0, b > 0.

Алгебраическое доказательство этого не равенства довольно простое:

(а – в)² ≥ 0;

Применим формулу «квадрат разности»:

а² - 2ав + в² ≥0;

Прибавим к обеим частям неравенства 4ав :

а² + 2ав + в² ≥4ав;

Применим формулу «квадрат суммы»:

(а + в)² ≥4ав;

Разделим обе части неравенства на 4 :

Так как а и в – положительные по условию, то извлечём из обеих частей неравенства квадратный корень:

Получили искомое выражение.

Рассмотрим геометрическое доказательство:

Дано: ABCD – прямоугольный, AD = a, AB = b, AK – биссектриса угла ВАD.

Доказать:

Доказательство:

1. АК – биссектриса, следовательно, ВАL = LAD. LAD и BLA – внутренние накрест лежащие углы при параллельных ВС и AD и секущей AL, то есть BLA = LAD.
2. В = 90°, следовательно, BAL = LAD = 45°, но BLA = LAD, значит, ∆ АВL – равнобедренный, BL = AB = b.
3. ∆AKD – равнобедренный, так как KD ┴ AD, DAL = 45°, значит AD = KD = a.

Очевидно, что , равенство достигается при

a = b , то есть ABCD – квадрат.

заменим в неравенстве а² на m , b² на n , получим

Или ,

то есть среднее геометрическое не больше среднего арифметического.

ДОКАЗАТЕЛЬСТВО НЕРАВЕНСТВ

Метод синтеза.

Это метод, основанный на получении (синтезировании) неравенства (которое требуется обосновать) из опорных (базисных) неравенств и методов их установления.

Решим задачу, используя метод синтеза

Задача 1. Докажите, что для любых неотрицательных a, b, c справедливо неравенство

Решение. Запишем три неравенства, устанавливающие зависимость между средним арифметическим и средним геометрическим двух неотрицательных чисел

Перемножим почленно полученные неравенства, так как их левая и правая части неотрицательны

Задача 2. Применим неравенство Коши к доказательству этого неравенства:

Метод использования тождеств .

Суть метода состоит в том, что данное неравенство путём равносильных преобразований приводится к очевидному тождеству.

Рассмотрим решение задачи этим методом.

Задача. Докажите, что для любых действительных чисел a и b справедливо неравенство .

Решение. Выделим в левой части неравенства полный квадрат

При любых действительных a и b это выражение неотрицательно, значит и данное неравенство выполнимо, то есть .

ЗАКЛЮЧЕНИЕ

Данная исследовательская работа была направлена на решение следующих задач:

• сбор информации и изучение различных методов и приемов доказательства неравенств;
• знакомство с замечательным неравенством Коши, его доказательство алгебраическим и геометрическим способом;
• применение полученных знаний для доказательства неравенств;
• знакомство с методом синтеза и использования тождеств в решении поставленных задач.

В процессе решения задач мы достигли поставленной цели нашей исследовательской работы –нахождение оптимально эффективного метода доказательства неравенств.

СПИСОК ЛИТЕРАТУРЫ

1. Алгебра. 8 класс: учеб. для учащихся общеобр. учрежд./ Ю.Н.Макарычев, Н.Г.Миндюк, К.И.Нешков, И.Е.Феоктистов.-13-е изд.- М.:Мнемозина,2013.-384с.

1. Алгебра. 8 класс. Дидактические материалы. Методические рекомендации/ И.Е.Феоктистов.-3-е изд.,стер.-М.:Мнемозина,2013.-173 с.

1. Мордкович А.Г. Алгебра. 8 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А.Г. Мордкович. – 10-е изд., стер. – М.: Мнемозина,2008. – 215с., С 185-200.

1. Берколайко С.Т. Использование неравенства Коши при решении задач.- М.: Квант, 1975.- №4.

Учебное заведение: МОУ Лицей№1 г.Комсомольск-на-Амуре

Руководитель: Будлянская Наталья Леонидовна

Если вы хотите участвовать в большой жизни, то наполняйте свою голову математикой, пока есть к тому возможность. Она окажет вам потом огромную помощь во всей вашей работе. (М.И. Калинин)

Представление левой части неравенства в виде суммы неотрицательных слагаемых (правая часть равна 0) с использованием тождеств.

Пример 1 . Доказать что для любого хϵR

Доказательство. 1 способ .

2 способ .

для квадратичной функции

что означает её положительность при любом действительном х .

Пример 2 . Доказать, что для любых x и y

Доказательство.

Пример 3 . Доказать, что

Доказательство.

Пример 4 . Доказать, что для любых a и b

Доказательство.

2. Метод от противного

Вот хороший пример применения данного метода.

Доказать, что для a, b ϵ R.

Доказательство.

Предположим, что.

Но,что явно доказывает, что наше предположение неверно.

Ч.Т.Д.

Пример 5 . Доказать, что для любых чисел А,В,С справедливо неравенство

Доказательство. Очевидно, что данное неравенство достаточно установить для неотрицательных А, В и С, так как будем иметь следующее отношения:

, что является обоснованием исходного неравенства.

Пусть теперь нашлись такие неотрицательные числа А, В и С , для которых выполняется неравенство

, что невозможно ни при каких действительных А,В и С . Сделанное выше предположение опровергнуто, что доказывает исследуемое исходное неравенство.

Использование свойств квадратного трехчлена

Метод основан на свойстве неотрицательности квадратного трехчлена, если

и.

Пример 6 . Доказать, что

Доказательство.

Пусть, a=2, 2>0

=>

Пример 7 . Доказать, что для любых действительных х и у имеет место быть неравенство

Доказательство. Рассмотрим левую часть неравенство как квадратный трехчлен относительно х:

, а>0, D

D= => P(x)>0 и

верно при любых действительных значениях х и у.

Пример 8 . Доказать, что

для любых действительных значениях х и у.

Доказательство. Пусть ,

Это означает, что для любых действительных у и неравенство

выполняется при любых действительных х и у.

Метод введения новых переменных или метод подстановки

Пример 9 . Доказать, что для любых неотрицательных чисел х, у, z

Доказательство. Воспользуемся верным неравенством для,

.

Получаем исследуемое неравенство

Использование свойств функций.

Пример 10 . Докажем неравенство

для любых а и b.

Доказательство. Рассмотрим 2 случая:

• Если а=b,то верно

причем равенство достигается только при а=b=0.

2)Если

, на R =>

()* ()>0, что доказывает неравенство

Пример 11 . Докажем, что для любых

Доказательство.

на R.

Если, то знаки чисел и совпадают, что означает положительность исследуемой разности =>

Применение метода математической индукции

Данный метод применяется для доказательства неравенств относительно натуральных чисел.

Пример 12 . Доказать, что для любого nϵN

• Проверим истинность утверждения при

- (верно)

2) Предположим верность утверждения при

(k>1)

3) Докажем истинность утверждения при n=k+1.

Сравним и: ,

Имеем:

Вывод: утверждение верно для любого nϵN.

Использование замечательных неравенств

• Теорема о средних (неравенство Коши)

• Неравенство Коши – Буняковского

• Неравенство Бернулли

Рассмотрим каждое из перечисленных неравенств в отдельности.

Применение теоремы о средних (неравенства Коши)

Среднее арифметическое нескольких неотрицательных чисел больше или равно их среднего геометрического

, где

Знак равенства достигается тогда и только тогда, когда

Рассмотрим частные случаи этой теоремы:

• Пусть n=2, тогда

• Пусть n=2, a>0, тогда

• Пусть n=3, тогда

Пример 13 . Доказать, что для всех неотрицательных a,b,c выполняется неравенство

Доказательство.

Неравенство Коши - Буняковского

Неравенство Коши - Буняковского утверждает, что для любых; справедливо соотношение

Доказанное неравенство имеет геометрическую интерпретацию. Для n=2,3 оно выражает известный факт, что скалярное произведение двух векторов на плоскости и в пространстве не превосходит произведение их длин. Для n=2 неравенство имеет вид: . Для n=3 получим

Пример 14.

Доказательство. Запишем исследуемое неравенство в следующем виде:

Это заведомо истинное неравенство, так как является частным случаем неравенства Коши – Буняковского.

Пример 15. Доказать, что для любых a,b,c ϵ R справедливо неравенство

Доказательство. Достаточно записать данное неравенство в виде

и сослаться на неравенство Коши – Буняковского.

Неравенство Бернулли

Неравенство Бернулли утверждает, что если х>-1, то для всех натуральных значений n выполняется неравенство

Неравенство может применяться для выражений вида

Кроме того, очень большая группа неравенств может быть легко доказана с помощью теоремы Бернулли.

Пример 16 .

Доказательство. Положив х=0,5 и применив теорему Бернулли для выражения

Получим требуемое неравенство.

Пример 17 . Доказать, что для любых n ϵ N

Доказательство.

по теореме Бернулли, что и требовалось.

Давида Гильберта спросили об одном из его бывших учеников. "А, такой-то? - вспомнил Гильберт. - Он стал поэтом. Для математики у него было слишком мало воображения.

Методы доказательства неравенств.

Решение неравенств. Равносильные неравенства.

Метод интервалов. Системы неравенств.

Доказательство неравенств. Существует несколько методов доказатель ства неравенств. Мы рассмотрим их на примере неравенства:

где a – положительное число.

1). Использование известного или ранее доказанного неравенства.

Известно, что ( a – 1 )² 0 .

2). Оценка знака разности между частями неравенства .

Рассмотрим разность между левой и правой частью:

более того, равенство имеет место только при a = 1 .

3). Доказательство от противного.

Предположим противное:

a , получим: a 2 + 1 < 2 a , т. e .

a 2 + 1 – 2 a < 0 , или ( a – 1 ) 2 < 0, что неверно. (Почему?) .

Полученное противоречие доказывает справедливость

Рассматриваемого неравенства.

4). Метод неопределённого неравенства.

Неравенство называется неопределённым , если у него знак \/ или /\ ,

т.е. когда мы не знаем в какую сторону следует повернуть этот знак,

чтобы получить справедливое неравенство.

Здесь действуют те же правила, что и с обычными неравенствами.

Рассмотрим неопределённое неравенство:

Умножая обе части неравенства на a , получим: a 2 + 1 \/ 2 a , т. e .

а 2 + 1 – 2 a \/ 0 , или ( a – 1) 2 \/ 0 , но здесь мы уже знаем, как повернуть

Знак \/ , чтобы получить верное неравенство (Как?). Поворачивая его

В нужном направлении по всей цепочке неравенств снизу вверх, мы
получим требуемое неравенство.

Решение неравенств. Два неравенства, содержащие одни и те же неизвестные, называются равносильными , если они справедливы при одних и тех же значениях этих неизвестных . Такое же определение используется для равносильности двух систем неравенств. Решение неравенств - это процесс перехода от одного неравенства к другому, равносильному неравенству. Для этого используются основные свойства неравенств (см. ). Кроме того, может быть использована замена любого выражения другим, тождественным данному. Неравенства могут быть алгебраические ( содержащие только многочлены ) и трансцендентные (например, логарифмические или тригонометрические ). Мы рассмотрим здесь один очень важный метод, используемый часто при решении алгебраических неравенств.

Метод интервалов. Решить неравенство: ( x – 3)( x – 5) < 2( x – 3). Здесь нельзя делить обе части неравенства на (x – 3), так как мы не знаем знака этого двучлена (он содержит неизвестное x ). Поэтому мы перенесём все члены неравенства в левую часть:

( x – 3)( x – 5) – 2( x – 3) < 0 ,

разложим её на множители:

( x – 3)( x – 5 – 2) < 0 ,

и получим: ( x – 3)( x – 7) < 0. Теперь определим знак произведения в левой части неравенства в различных числовых интервалах. Заметим, что x = 3 и x = 7 - корни этого выражения. Поэтому вся числовая ось разделится этими корнями на следующие три интервала:

В интервале I (x < 3 ) оба сомножителя отрицательны, следовательно , их произведение положительно ; в интервале II (3 < x < 7 ) первый множитель (x – 3 ) положителен, а второй (x – 7 ) отрицателен, поэтому их произведение отрицательно ; в интервале III (x > 7 ) оба сомножителя положительны, следовательно, их произведение также положительно . Теперь остаётся выбрать интервал, в котором наше произведение отрицательно . Это интервал II , следовательно, решение неравенства: 3 < x < 7. Последнее выражение - так называемое двойное неравенство . Оно означает, что x должен быть одновременно больше 3 и меньше 7.

П р и м е р. Решить следующее неравенство методом интервалов:

( x – 1)(x – 2)(x – 3) … (x –100) > 0 .

Р е ш е н и е. Корни левой части неравенства очевидны: 1, 2, 3, …, 100.

Они разбивают числовую ось на 101 интервал:

Так как количество скобок в левой части чётно (равно 100), то

При x < 1, когда все множители отрицательны, их произведение

Положительно. При переходе через корень происходит смена

Знака произведения. Поэтому следующим интервалом, внутри

Которого произведение положительно, будет (2, 3), затем (4, 5),

Затем (6, 7), … , (98, 99) и наконец , x >100.

Таким образом, данное неравенство имеет решение:

x < 1, 2 < x < 3, 4 < x < 5 ,…, x >100.

Итак, чтобы решить алгебраическое неравенство, надо перенести все его члены в левую (или правую) часть и решить соответствующее уравнение. После этого найденные корни нанести на числовую ось; в результате она разбивается на некоторое число интервалов. На последнем этапе решения нужно определить, какой знак имеет многочлен внутри каждого из этих интервалов, и выбрать нужные интервалы в соответствии со знаком решаемого неравенства.

Заметим, что большинство трансцендентных неравенств заменой неизвестного приводятся к алгебраическому неравенству. Его надо решить относительно нового неизвестного, а затем путём обратной замены найти решение для исходного неравенства.

Системы неравенств. Чтобы решить систему неравенств, необходимо решить каждое из них, и совместить их решения. Это совмещение приводит к одному из двух возможных случаев: либо система имеет решение, либо нет.

П р и м е р 1. Решить систему неравенств:

Р е ш е н и е. Решение первого неравенства: x < 4 ; а второго: x > 6.

Таким образом, эта система неравенств не имеет решения.

(Почему?)

П р и м е р 2. Решить систему неравенств:

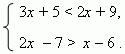
Р е ш е н и е. Первое неравенство, как и прежде, даёт: x < 4; но решение

Второго неравенства в данном примере: x > 1.

Таким образом, решение системы неравенств: 1 < x < 4.

МОУ Гришино -Слободская средняя общеобразовательная школа

Программа модуля

« Методы доказательства неравенств»

в рамках элективного курса

«За страницами учебника математики»

для учащихся 10-11 классов

Составил:

учитель математики

Панкова Е.Ю

Пояснительная записка

«Математику называют тавтологической наукой: другими словами, про математиков говорят, что они тратят время на доказательство того, что предметы равны самим себе. Это утверждение весьма неточно по двум причинам. Во-первых, математика, несмотря на свойственный ей научный язык, не является наукой; скорее ее можно назвать искусством. Во- вторых основные результаты математики чаще выражаются неравенствами, а не равенствами.»

Неравенства используются в практической работе математика постоянно. Они применяются для получения ряда интересных и важных экстремальных свойств «симметричных» фигур: квадрата, куба, равностороннего треугольника, а также для доказательства сходимости итерационных процессов и вычисления некоторых пределов. Важна роль неравенств и в различных вопросах естествознания и техники.

Задачи на доказательство неравенств самые трудные и интересные из традиционных. Доказательства неравенств требуют истинной изобретательности, творчества, которые делают математику тем захватывающим воображение предметом, каким она является.

Обучение доказательствам играет большую роль в развитии дедуктивно- математического мышления и общих мыслительных способностей учащихся. Как же научить школьников самостоятельно проводить доказательства неравенств? Ответ гласит: только путем рассмотрения многих приемов и методов доказательств и регулярного их применения.

Применяемые для доказательства неравенств идеи почти столь же разнообразны, как и сами неравенства. В конкретных ситуациях общие методы часто приводят к некрасивым решениям. Но неочевидное комбинирование нескольких «базовых» неравенств удается лишь немногим школьникам. И, кроме того, ничто не мешает ученику в каждом конкретном случае поискать лучшее решение, нежели полученное общим методом. По этой причине доказательства неравенств нередко относят к области искусства. И как во всяком искусстве здесь есть свои технические приемы, набор которых весьма широк и овладеть всеми очень сложно, но каждый учитель должен стремится к расширению имеющегося в его запасе математического инструмента.

Данный модуль рекомендуется для учащихся 10-11 классов. Здесь рассматриваются не все возможные методы доказательства неравенств (не затронуты метод замены переменной, доказательство неравенств с помощью производной, метод исследования и обобщения, прием упорядочения). Предложить рассмотреть остальные методы можно на втором этапе (например, в 11 классе), если данный модуль курса вызовет интерес у учащихся, а также ориентируясь на успехи усвоения первой части курса.

		Уравнения и неравенства с параметром.
		Методы доказательства неравенств.
		Уравнения и неравенства, содержащие неизвестное под знаком модуля.
		Системы неравенств с двумя переменными.

Содержание элективного курса

«За страницами учебника математики»

«Методы доказательства неравенств»

		Введение.
		Доказательство неравенств на основании определения.
		Метод математической индукции.
		Применение классических неравенств.
		Графический метод.
		Метод от противного.
		Прием рассмотрения неравенств относительно одной из переменных.
		Идея усиления.
		Урок - контроль.

Урок1. Введение.

Доказательство неравенств -увлекательная и непростая тема элементарной математики. Отсутствие единого подхода к проблеме доказательства неравенств, приводит к поиску ряда приемов, пригодных для доказательства неравенств определенных видов. На данном элективном курсе будут рассматриваться следующие методы доказательства неравенств:

Повторение:

Провести доказательства некоторых свойств.

Классические неравенства:

1)
(неравенство Коши)

4)

Историческая справка:

Неравенство (1) называют в честь французского математика Огюста Коши. Число
называют средним арифметическим чисел a и b;

число
называют средним геометрическим чисел a и b. Таким образом, неравенство означает, что среднее арифметическое двух положительных чисел не меньше их среднего геометрического.

Дополнительно:

Рассмотреть несколько математических софизмов с неравенствами.

Математический софизм - удивительное утверждение, в доказательстве которого кроются незаметные, а подчас и довольно тонкие ошибки.

Софизмы – это ложные результаты, полученные с помощью рассуждений, которые только кажутся правильными, но обязательно содержат ту или иную ошибку.

Пример:

Четыре больше двенадцати

Урок2.Доказательство неравенств на основании определения.

Суть этого метода заключается в следующем: для того чтобы установить справедливость неравенства F(x,y,z)>S(x,y,z) составляют разность F(x,y,z)-S(x,y,z) и доказывают, что она положительна. Применяя этот метод, часто выделяют квадрат, куб суммы или разности, неполный квадрат суммы или разности. Это помогает определить знак разности.

Пример. Доказать неравенство (x+y)(x+y+2cosx)+2 2sin 2 x

Доказательство:

Рассмотрим разность (x+y)(x+y+2cosx)+2- 2sin 2 x =(x+y)(x+y+2cosx)+2cos 2 x=(x+y)(x+y+2cosx)+ cos 2 x +cos 2 x= (x+y) 2 +2(x+y)cosx+ cos 2 x +cos 2 x=((x+y)+cosx) 2 + cos 2 x 0.

Доказать неравенство:

1.ab(a+b)+bc(b+c)+ac(a+c) 6abc

3.

4.
>2x-20

5.

6.(a+b)(b+c)(c+a) 8abc

Урок3.Метод математической индукции.

При доказательстве неравенств, в которые входят натуральные числа часто прибегают к методу математической индукции. Метод состоит в следующем:

1) проверяем истинность теоремы для n=1;

2)допускаем, что теорема верна для некоторого n=k, и исходя из этого допущения доказываем истинность теоремы для n=k+1;

3) на основании первых двух шагов и принципа математической индукции заключаем, что теорема верна для любого n.

Пример.

Доказать неравенство

Доказательство:

1) при n=2 неравенство верно:

2)Пусть неравенство верно для n=k т.е.
(*)

Докажем, что неравенство верно при n=k+1, т.е.
. Умножим обе части неравенства (*) на
получим 3)Из п1.и п.2 делаем вывод, что неравенство верно для любого n.

Задания для работы в классе и дома

Доказать неравенство:

1)

2)

3)

4)

5)

6)
.

Урок4. Применение классических неравенств.

Суть этого метода заключается в следующем: с помощью ряда преобразований выводят требуемое неравенство с помощью некоторых классических неравенств.

Пример.

Доказать неравенство:

Доказательство:

В качестве опорного неравенства используем .

Приведем данное неравенство к следующему виду:

, тогда

Но =
, тогда

Доказать неравенство:

1)(p+2)(q+2)(p+q)16pq(для док-ва используется неравенство
)

2)
(для док-ва используется неравенство )

3) (a+b)(b+c)(c+a) 8abc (для док-ва используется неравенство )

4) (для док-ва используется неравенство ).

Урок5. Графический метод.

Доказательство неравенств графическим методом заключается в следующем: если доказываем неравенство f(x)>g(x)(f(x)

1) построить графики функций y=f(x) и y=g(x);

2)если график функции y=f(x) расположен выше (ниже) графика функции y=g(x), то доказываемое неравенство верно.

Пример.

Доказать неравенство:

cosx
,x0

Доказательство:

Построим в одной системе координат графики функций y=cosx и

Из графика видно, что при x0 график функции y=cosx лежит выше графика функции y= .

Задания для работы в классе и дома.

Доказать неравенство:

1)

4)
.

Урок6.Метод от противного

Суть этого метода заключается в следующем: пусть нужно доказать истинность неравенства F(x,y,z) S(x,y,z)(1). Предполагают противное, т. е что хотя бы для одного набора переменных справедливо неравенство F(x,y,z) S(x,y,z) (2). Используя свойства неравенств, выполняют преобразования неравенства (2). Если в результате этих преобразований получается ложное неравенство, то это означает, что предположение о справедливости неравенства (2) неверно, а потому верно неравенство (1).

Пример.

Доказать неравенство:

Доказательство:

Предположим противное, т. е .

Возведем обе части неравенства в квадрат, получим , откуда
и далее

. Но это противоречит неравенству Коши. Значит наше предположение неверно, т. е справедливо неравенствоЗадания для работы в классе и дома.

Урок9. Урок- контроль знаний учащихся.

Работу на этом уроке можно организовать в парах или если большая численность класса в группах. В конце урока каждый учащийся должен быть оценен. Это и есть зачетная форма по данному курсу. По данной теме не рекомендуется проводить контрольную работу т.к. доказательство неравенств, как это уже говорилось в пояснительной записке, относят к области искусства. В начале учащимся предлагается самим определить метод доказательства предложенных неравенств. Если же у учащихся возникнут затруднения, то учитель сообщаем им рациональный метод, предупредив группу, что это, конечно же, повлияет на их оценку.

Работа по парам.

Примеры заданий.

________________________________________________________________

Доказать неравенство:

1.
(метод мат. индукции)

2.
(по определению)

Модулем . Уравнения и неравенства с па­раметрами. ... свойств, формулировка и доказательство теорем, вывод формул... простейшие неравенства . 7. Уметь пользоваться методом интервалов...

Программа Открытой олимпиады и требования к подготовке по математике для учащихся 9 классов

Программа

Понятие модуля действительного числа. Арифметическое и геометрическое определения модуля . Раскрытие модулей . ... неравенства . Доказательство неравенств . Решение линейных, квадратных, дробно-рациональных неравенств с одной переменной. Решение неравенств ...

Программа факультатива по математике для 8 класса

Программа

Продемонстрировать методы доказательства чуть более сложных неравенств с помощью этого простого неравенства ? Итак, в этой министерской программе ...

Редкая олимпиада обходится без задач, в которых требуется доказать некоторое неравенство. Алгебраические неравенства доказываются с помощью различных методов, которые основываются на равносильных преобразованиях и свойствах числовых неравенств:

1) если a – b > 0, то a > b; если a – b

2) если a > b, то b a;

3) если a

4) если a

5) если a 0, то ac

6) если a bc; a / c > b / c ;

7) если a 1

8) если 0

Напомним некоторые опорные неравенства, которые часто используются для доказательства других неравенств:

1) а 2 > 0;

2) aх 2 + bx + c > 0, при а > 0, b 2 – 4ac

3) x + 1 / x > 2, при х > 0, и x + 1 / x –2, при х

4) |a + b| |a| + |b|, |a – b| > |a| – |b|;

5) если a > b > 0, то 1 / a

6) если a > b > 0 и х > 0, то a x > b x , в частности, для натурального n > 2

a 2 > b 2 и n √ a > n √b ;

7) если a > b > 0 и х

8) если х > 0, то sin x

Многие задачи олимпиадного уровня, и это не только неравенства, эффективно решаются с помощью некоторых специальных неравенств, с которыми учащиеся школы часто не бывают знакомы. К ним, прежде всего, следует отнести:

• неравенство между средним арифметическим и средним геометрическим положительных чисел (неравенство Коши):

• неравенство Бернулли:

(1 + α) n ≥ 1 + nα, где α > -1, n – натуральное число;

• неравенство Коши – Буняковского:

(a 1 b 1 + a 2 b 2 + . . . + a n b n) 2 ≤ (a 1 2 + a 2 2 + . . . + a n 2)(b 1 2 + b 2 2 + . . . + b n 2);

К наиболее «популярным» методам доказательства неравенств можно отнести:

• доказательство неравенств на основе определения;
• метод выделения квадратов;
• метод последовательных оценок;
• метод математической индукции;
• использование специальных и классических неравенств;
• использование элементов математического анализа;
• использование геометрических соображений;
• идея усиления и др.

Задачи с решениями

1. Доказать неравенство:

а) a 2 + b 2 + c 2 + 3 > 2 · (a + b + c);

б) a 2 + b 2 + 1 > ab + a + b;

в) x 5 + y 5 – x 4 y – x 4 y > 0 при x > 0, y > 0.

а) Имеем

a 2 + b 2 + c 2 + 1 + 1 + 1 – 2a – 2b – 2c = (a – 1) 2 + (b – 1) 2 + (c – 1) 2 > 0,

что очевидно.

б) Доказываемое неравенство после умножения обеих частей на 2 принимает вид

2a 2 + 2b 2 + 2 > 2ab + 2a + 2b,

или

(a 2 – 2ab + b 2) + (a 2 – 2a + 1) + (b 2 – 2b +1) > 0,

или

(a – b) 2 + (a – 1) 2 + (b – 1) 2 > 0,

что очевидно. Равенство имеет место лишь при a = b = 1.

в) Имеем

x 5 + y 5 – x 4 y – x 4 y = x 5 – x 4 y – (x 4 y – y 5) = x 4 (x – y) – y 4 (x – y) =

= (x – y) (x 4 – y 4) = (x – y) (x – y) (x + y) (x 2 + y 2) = (x – y) 2 (x + y) (x 2 + y 2) > 0.

2. Доказать неравенство:

а)	a	+	b		>	2 при a > 0, b > 0;
	b		a

б)	Р	+	Р	+	Р		> 9, где a, b, c – стороны и P – периметр треугольника;
	a		b		c

в) ab(a + b – 2c) + bc(b + c – 2a) + ac(a + c – 2b) > 0, где a > 0, b > 0, c > 0.

а) Имеем:

a	+	b	– 2 =	a 2 + b 2 – 2ab	=	(a – b) 2		> 0.
b		a		ab		ab

б ) Доказательство данного неравенства элементарно следует из следующей оценки:

b + c	+	a + c	+	a + b	=
a		b		c

=

b

+

c

+

a

+

c

+

a

+

b

=

a

a

b

b

c

c

= (

b

+

a

) + (

c

+

a

) + (

c

+

b

) > 6,

a

b

a

c

b

c

Равенство достигается для равностороннего треугольника.

в) Имеем:

ab(a + b – 2c) + bc(b + c – 2a) + ac(a + c – 2b) =

= abc (

a

+

b

– 2 +

b

+

c

– 2 +

a

+

c

– 2 ) =

c

c

a

a

b

b

= abc ((

a

+

b

– 2) + (

a

+

c

– 2) + (

b

+

c

– 2) ) > 0,

b

a

c

a

c

b

так как сумма двух положительных взаимно обратных чисел больше или равна 2.

3. Доказать, что если a + b = 1, то имеет место неравенство a 8 + b 8 > 1 / 128 .

Из условия, что a + b = 1, следует, что

a 2 + 2ab + b 2 = 1.

Сложим это равенство с очевидным неравенством

a 2 – 2ab + b 2 > 0.

Получим:

2a 2 + 2b 2 > 1, или 4a 4 + 8a 2 b 2 + 4b 2 > 1.

4a 4 – 8a 2 b 2 + 4b 2 > 0,

получим:

8a 4 + 8b 4 > 1, откуда 64a 8 + 128a 4 b 4 + 64b 4 > 1.

Сложив это неравенство с очевидным неравенством

64a 8 – 128a 4 b 4 + 64b 4 > 0,

получим:

128a 8 + 128 b 8 > 1 или a 8 + b 8 > 1 / 128 .

4. Что больше е е · π π или е 2 π ?

Рассмотрим функцию f(x) = x – π · ln x . Поскольку f’(x) = 1 – π / х , и слева от точки х = π f’(x) 0, а справа - f’(x) > 0, то f(x) имеет наименьшее значение в точке х = π . Таким образом f(е) > f(π) , то есть

е – π · ln е = е – π > π – π · ln π

или

е + π · ln π > 2π .

Отсюда получаем, что

е е + π · ln π > е 2 π ,

е е · е π · ln π > е 2 π ,

е е · π π > е 2 π .

5. Доказать, что

lg (n + 1) >	lg 1 + lg 2 + . . . + lg n	.
	n

Используя свойства логарифмов, нетрудно свести данное неравенство к равносильному неравенству:

(n + 1) n > n!,

где n! = 1 · 2 · 3 · . . . · n (n-факториал). Кроме того имеет место система очевидных неравенств:

n + 1 > 1,

n + 1 > 2,

n + 1 > 3,

. . . . .

n + 1 > n,

после почленного умножения которых, непосредственно получаем, что (n + 1) n > n!.

6. Доказать, что 2013 2015 · 2015 2013

Имеем:

2013 2015 · 2015 2013 = 2013 2 · 2013 2013 · 2015 2013 =

2013 2 · (2014 – 1) 2013 · (2014 + 1) 2013

Очевидно, так же можно получить общее утверждение: для любого натурального n выполняется неравенство

(n – 1) n +1 (n + 1) n –1

7. Докажите, что для любого натурального числа n выполняется неравенство:

1	+	1	+	1	+ . . . +	1		2n – 1	.
1!		2!		3!		n!		n

Оценим левую часть неравенства:

1	+	1	+	1	+ . . . +	1	=
1!		2!		3!		n!

= 1 +	1	+	1	+	1	+ . . . +	1
	1 · 2		1 · 2 · 3		1 · 2 · 3 · 4		1 · 2 · 3 · . . . · n

1 +	1	+	1	+	1	+ . . . +	1	=
	1 · 2		2 · 3		3 · 4		(n – 1) · n

= 1 + (1 –	1	) + (	1	–	1	) + (	1	–	1	) + . . . + (	1	–	1	) = 2 –	1	,
	2		2		3		3		4		n – 1		n		n

что и требовалось доказать.

8. Пусть а 1 2 , а 2 2 , а 3 2 , . . . , а n 2 – квадраты n различных натуральных чисел. Докажите, что

(1 –	1	) (1	–	1	) (1	–	1	) . . . (1	–	1	) >	1	.
	а 1 2			а 2 2			а 3 2			а n 2		2

Пусть наибольшее из этих чисел равно m. Тогда

(1 –	1	) (1	–	1	) (1	–	1	) . . . (1	–	1	) >
	а 1 2			а 2 2			а 3 2			а n 2

> (1 –	1	) (1	–	1	) (1	–	1	) . . . (1	–	1	) ,
	2 2			3 2			4 2			m 2

так как в правую часть добавлены множители, меньшие 1. Вычислим правую часть, разложив каждую скобку на множители:

=	2 · 3 2 · 4 2 · . . . · (m – 1) 2 · (m + 1)	=	m + 1	=	1	+	1	>	1	.
	2 2 · 3 2 · 4 2 · . . . · m 2 Раскрыв в левой части скобки, получим сумму 1 + (a 1 + . . . + a n) + (a 1 a 2 + . . . + a n –1 a n) + (a 1 a 2 a 3 + . . . + a n –2 a n –1 a n) + . . . + a 1 a 2 . . . a n . Сумма чисел во второй скобке не превосходит (a 1 + . . . + a n) 2 , сумма в третьей скобке не превосходит (a 1 + . . . + a n) 3 , и так далее. Значит, все произведение не превосходит 1 + 1 / 2 + 1 / 4 + 1 / 8 + . . . + 1 / 2 n = 2 – 1 / 2 n Способ 2. Методом математической индукции докажем, что для всех натуральных n верно неравенство: (1 + a 1) . . . (1 + a n) При n = 1 имеем: 1 + a 1 1 . Пусть при n = k имеет место: (1 + a 1 ) . . . (1 + a k ) 1 + . . . + a k ). Рассмотрим случай n = k +1: (1 + a 1 ) . . . (1 + a k )(1 + a k +1 ) (1 + 2(a 1 + . . . + a k ))(1 + a k +1 ) ≤ 1 + 2(a 1 + . . . + a k ) + a k +1 (1 + 2 · 1 / 2) = 1 + 2(a 1 + . . . + a k + a k +1 ). В силу принципа математической индукции неравенство доказано. 10. Доказать неравенство Бернулли: (1 + α) n ≥ 1 + nα, где α > -1, n – натуральное число. Воспользуемся методом математической индукции. При n = 1 получаем истинное неравенство: 1 + α ≥ 1 + α. Предположим, что имеет место неравенство: (1 + α) n ≥ 1 + nα. Покажем, что тогда имеет место и (1 + α) n + 1 ≥ 1 + (n + 1)α. Действительно, поскольку α > –1 влечет α + 1 > 0, то умножая обе части неравенства (1 + α) n ≥ 1 + nα на (a + 1), получим (1 + α) n (1 + α) ≥ (1 + nα)(1 + α) или (1 + α) n + 1 ≥ 1 + (n + 1)α + nα 2 Поскольку nα 2 ≥ 0, следовательно, (1 + α) n + 1 ≥ 1 + (n + 1)α + nα 2 ≥ 1 + (n + 1)α. Таким образом, согласно принципу математической индукции, неравенство Бернулли справедливо. Задачи без решений 1. Доказать неравенство для положительных значений переменных a 2 b 2 + b 2 c 2 + a 2 c 2 ≥ abc(a + b + c). 2. Доказать, что при любом a имеет место неравенство 3(1 + a 2 + a 4) ≥ (1 + a + a 2) 2 . 3. Доказать, что многочлен x 12 – x 9 + x 4 – x + 1 при всех значениях x положителен. 4. Для 0 e доказать неравенство (e + x) e – x > (e – x) e + x . 5. Пусть a, b ,c – положительные числа. Докажите, что a + b + b + c + a + c ≤ 1 + 1 +